Topic outline

• digi.komp12 Beispiel

  Collapse all Expand all
  

  Mathematik
  

  Winkelfunktionen-Harmonische Schwingung
  

  10./11./12. Schulstufe

   

  
  

  
  

  • Mark as done

    Aufgabe 1

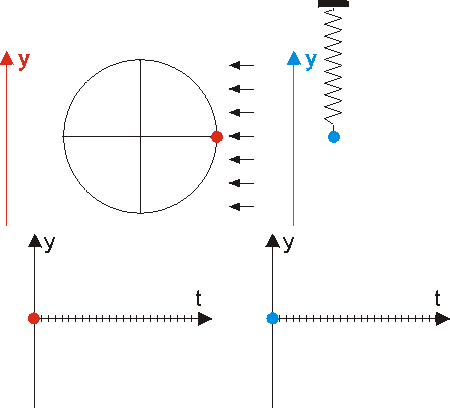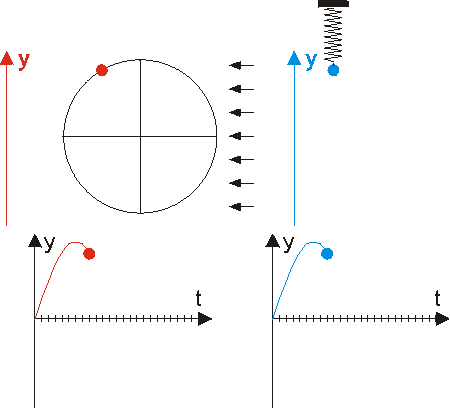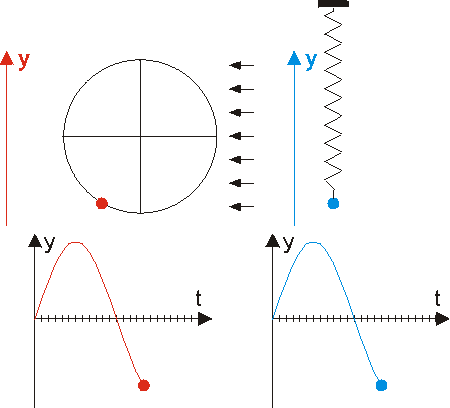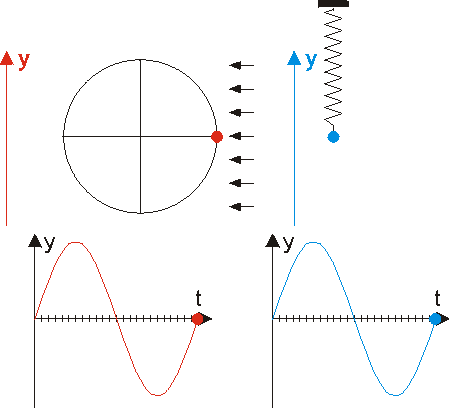
    Die Graphen der Winkelfunktionen kann man mit Hilfe des Einheitskreises zeichnen. Verwende dieses GeoGebra-Applet, um die folgenden Fragen zu beantworten.

    • In welchen Quadranten ist der Sinus positiv?
    • In welchen Quadranten ist der Cosinus negativ?
    • Was ist sin(0°)?
    • Was ist cos(180°)?
    • Was ist sin(180°)?
    • Was ist cos(270°)?

    Teste hier dein Wissen über Sinus und Cosinus im Einheitskreis.
  • Mark as done

    Harmonische Schwingungen: 

    Sinusfunktionen können Schwingungsvorgänge beschreiben. Man verwendet dazu folgende Begriffe:

    • Amplitude r: größte Entfernung des schwingenden Körpers von der Ruhelage (Einheit: 1m)
    • Schwingungsdauer T: Zeitdauer einer vollen Schwingung (Einheit: 1s)
    • Frequenz f: Zahl der Schwingungen pro Sekunde (Einheit: 1 Hertz)
    • Elongation s(t) zum Zeitpunkt t: Der mit Vorzeichen versehene Abstand des Körpers von der Ruhelage zum Zeitpunkt t (Einheit: 1m)

    
    

    Die Frequenz ist der Kehrwert der Schwingungsdauer: f = 1 / T

  • Mark as done

    Aufgabe 2

    f(x) = a . sin(b . x)
    Welche Bedeutungen haben die Parameter a und b? Experimentiere mit diesem GeoGebra-Applet.

    Überprüfe dein Wissen hier!
    Und danach hier!
  • Mark as done

    Aufgabe 3

    In einem Atemzug atmet ein erwachsener Mensch durchschnittlich 0,5l Luft ein. Die Geschwindigkeit eines gleichmäßigen Atemvorgangs eines Menschen zum Zeitpunkt t wird durch die Funktion v(t) = 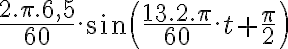$\frac{2.\pi.6,5 }{60} . sin( \frac{13.2. \pi }{60} .t+ \frac{\pi}{2} )$ modelliert
    (t in s, v in l/s).
    Zeichne den Funktionsgraphen mit GeoGebra.

    • Berechne v für t = 12s und t = 30s und interpretiere dein Ergebnis.
      
    • Wie viele Atemzyklen (vollständiges Ein- und Ausatmen) hat dieser Mensch pro Minute?
    • Wie lange benötigt dieser Mensch für einen vollständigen Atemzyklus?
    • Berechne die maximale Atemgeschwindigkeit dieses Menschen.
    • Berechne die erste Nullstelle dieser Funktion. Was bedeutet die Nullstelle in diesem Kontext?

     

     

    Überprüfe deine Lösungen mit Hilfe der Videoanleitung!

• Metadaten

  Informationen für Lehrkräfte

  Fachbezug	Mathematik
  Bezug zum Fachlehrplan	Sinus und Cosinus im Einheitskreis darstellen können. Die Sinus- und Cosinusfunktion und deren Graphen kennen. Wichtige Eigenschaften an deren Graphen ablesen können. Den typischen Verlauf von Funktionen f der Form f(x)=a.sin(b.x+c) kennen und die Paramter im Kontext interpretieren können (insbesondere bei Schwingungsvorgängen).
  Schulstufe	10./11./12. Schulstufe
  Zeitaufwand	1-2 Unterrichtseinheiten
  Handlungsdimension	Wissen und Verstehen Anwenden und Gestalten Reflektieren und Bewerten
  Digitale Kompetenzen	Betriebssysteme und Standard-Andwendungen Tabellenkalkulation - GeoGebra
  Anmerkung	Material- und Medienbedarf GeoGebra

  • Mark as done

    

    Dieses Werk von Michaela Streuselberger für www.digikomp.at steht unter einer Creative Commons Namensnennung 3.0 Unported Lizenz.

  • 

    Download des digi.komp-Beispiels als Moodle-Kurssicherung File

    Mark as done